Jak vydělat v ruletě
Návod, jak by se opravdu a legálně dalo vydělat v ruletě, a to na nerovnosti či nevyváženosti ruletového kola. K poznání, zda je ruletové kolo nerovné, a zdali tedy některá čísla mají tendenci padat častěji, nám pomůže statistika. Ovšem nebudeme vás nutit nic počítat, výpočty jsou již připraveny i s podrobným komentářem.
Vyváženost ruletového kola jsme již řešili, a to na obě strany – to znamená, že některá čísla padala velmi zřídka nebo velmi často. Dnes nás bude zajímat jen druhý případ, protože jen čísla, která se objevují častěji než by bylo zdrávo (to rozhodne statistika s určitou pravděpodobností, kterou si předem zvolíme), pro nás mají význam.
Jednoduše na čísla, která se často vyskytují, můžeme začít sázet – buď na jedno číslo, nebo pokrývat určitý úsek ruletového kola (několik čísel vedle sebe), například jednu osminu (asi 5 čísel vedle sebe), jednu čtvrtinu (asi 9 čísel) nebo jednu třetinu kola (asi 12 sousedících čísel).
 Ještě bychom mohli předeslat, že inteligentní hráč upřednostní francouzskou ruletu, kde je 37 čísel, před ruletou americkou, kde je čísel 38 (navíc je tzv. dvojitá nula).
Ještě bychom mohli předeslat, že inteligentní hráč upřednostní francouzskou ruletu, kde je 37 čísel, před ruletou americkou, kde je čísel 38 (navíc je tzv. dvojitá nula).
Ruleta se dnes hraje buď pomocí mechanického nebo elektronického či elektromechanického zařízení. Nerovností či nevyvážeností kola myslíme jak mechanické, byť mikroskopické, nerovnosti, díky kterým mají čísla v určitém úseku ruletového kola tendenci padat častěji, nebo špatný generátor náhodných čísel v případě elektronických verzí, kdy generovaná čísla by po určité době mohla projevovat jisté zákonitosti.
Právě těchto nedokonalostí by se dalo využít, i když je pravděpodobné, že kasina budou mít vyváženost mechanického kola a generátory náhodných čísel dobře ošetřeny a mj. zkontrolovány statistickými testy. To nás ale nemusí odradit, trocha námahy se může vyplatit.
Začínáme
Máte k dispozici, nebo získáte data, která zachycují například posledních 10 tisíc vytočených čísel. Vzorek může být i menší, ale větší počet dat má lepší vypovídací schopnost. Víte tedy, kolikrát které číslo padlo, slovy statistiky znáte absolutní četnosti každého čísla. Čísla si seřadíte podle toho, jak jdou na ruletovém kole za sebou – viz obrázek ruletového kola výše nebo následující obrázek.
![]()
Každému číslu přidělíte jeho četnost výskytu (vše jde zvládnout třeba pomocí Excelu). Zvolíte úsek kola, který chcete sledovat, například 9 čísel vedle sebe, které pokrývají zhruba 1/4 ruletového kola (9/37). Sečtete četnosti výskytu prvních devíti čísel, pak se posunete o jedno do strany (třeba doprava) a sečtete četnosti dalších devíti čísel.
Devět sousedících čísel (či zhruba 1/4 kola), která mají největší četnost, je to, co hledáte. Do tohoto úseku zapadá kulička rulety nejčastěji. Nyní jde o to rozhodnout, zda je to ještě „normální“, nebo již statisticky významné.
Záleží přitom na počtu roztočení rulety (spinů) a úseku, který sledujeme – viz Tabulka 1 a Tabulka 2. Pak by bylo možné na tento úsek kola s výhodou sázet. Jak? Jednoduše bychom vsadili na každé jednotlivé číslo z tohoto úseku stejnou sumu peněz, například po jednom dolaru.
Kdy čísla padají příliš často z pohledu statistiky a pravděpodobnosti
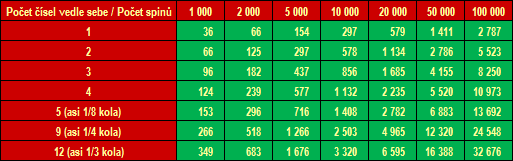
Tabulka 1 uvádí kritické horní hranice pro různé úseky ruletového kola a různé počty spinů. Pro zajímavost jsou v tabulce uvedeny hodnoty také pro jedno jediné číslo, dvě sousedící čísla atd., pak následují větší úseky.
Výsledky v Tabulce 1 říkají, že s pravděpodobností 95 % bude četnost výskytu čísla nebo určitého počtu čísel vedle sebe (sousedících čísel) stejná nebo nižší než v tabulce. Lépe pochopíme na konkrétním případu.
Podívejme se třeba na souřadnici [1 číslo a 10 000 spinů]: 297 výskytů. To znamená, že je 95procentní pravděpodobnost, že jedno jediné číslo při deseti tisíci spinech padne 0× (vůbec) až 297× (tj., že četnost výskytu tohoto čísla bude 0 až 297). Z toho vyplývá, že pravděpodobnost, že jedno číslo padne 298× a více, je pouhých 5 procent (jazykem statistiky: 298× a více je tzv. kritická oblast při hladině významnosti 5 %).
Ve statistice nás většinou zajímá posledních 5 % nebo 1 % hodnot (tak zvaně volíme tyto hladiny významnosti). Pokud nějaké číslo nebo úsek čísel padá do této kritické oblasti, pak je pouze 5procentní resp. 1procentní pravděpodobnost, že kolo je dobře vyváženo, tedy že to není náhoda. Právě na tom bychom mohli v ruletě vydělat, jak ukazují příklady pod tabulkou.
Tabulka 1: Kritické horní hranice pro různé úseky kola a počty spinů (pravděpodobnost 95 %)
Příklad – jak vydělat na sázce na 1 číslo
Zůstaňme na chvíli pro jednoduchost a lepší ilustraci u sázky na 1 číslo. Jedno libovolné číslo by teoreticky mělo padat s pravděpodobností 1/37 (francouzská ruleta má 37 čísel). Avšak zaznamenáme-li například, že určité číslo padlo 300× z 10 000 spinů (tj. více než 297×, tedy do kritické oblasti), pak je jen 5procentní pravděpodobnost, že je to náhoda a že kolo je ve skutečnosti dobře vyvážené.
S tímto rizikem pak můžeme předpokládat, že určité číslo ve skutečnosti padá s pravděpodobností 300/10000 = 0,03 (to je tzv. relativní četnost, kterou použijeme jako odhad skutečné pravděpodobnosti) namísto teoretické pravděpodobnosti 1/37 = 0,027. Co to mění? Můžeme si nyní spočítat, jak bychom na tom byli při dlouhodobém sázení:
EV = 0,03 × $35 + (1 - 0,03) × (-$1) = $0,08 (zisk hráče 8 %, ztráta kasina 8 %).
Vzorec říká následující. Pokud bychom na to číslo sázeli $1, pak s pravděpodobností 0,03 můžeme vyhrát $35 (to je výplatní poměr na jedno číslo) a s pravděpodobností 0,97 (doplněk do jedné) prohrát jeden vsazený dolar (-$1). To je tzv. očekávaná hodnota (EV – Expected Value); vážený průměr, kde váhami jsou pravděpodobnosti; výsledek, který můžeme očekávat při dlouhodobém sázení.
Z každého vsazeného $1 na toto číslo bychom v dlouhodobém průměru vydělali 8 centů ($0,08), jinými slovy 8 %.
Přitom principem hazardních her je, že hráč má zápornou očekávanou hodnotu: teoreticky bychom měli vyhrát s pravděpodobností 1/37 a prohrát s pravděpodobností 36/37, tj. prodělat 2,7 %:
EV = 1/37 × $35 + (1 - 1/37) × (-$1) = -$0,027 (ztráta hráče 2,7 %, zisk kasina 2,7 %).
Příklad – jak vydělat na pokrytí 1/3 kola
Stejný závěr jako pro 1 číslo platí i pro ostatní úseky ruletového kola. Stačí se podívat do Tabulky 1, případně do Tabulky 2 (viz následující kapitola). Pokrýt třetinu kola rulety znamená vsadit na 12 sousedních čísel. Jakákoliv třetina kola by měla padat s pravděpodobností 12/37.
Samozřejmě si vyberete třetinu kola, jejíž čísla dohromady padají nejčastěji (mají nejvyšší celkovou četnost). Pak pomocí Tabulky 1 otestujete, zda čísla z této třetiny (dohromady) opravdu padají s touto pravděpodobností.
Například při 5000 spinech je 95procentní pravděpodobnost, že čísla z této třetiny padnout maximálně 1676×. Jinými slovy je pouze 5procentní pravděpodobnost, že by třetina kola padla 1677× a více (kritická oblast) – v tomto případě bychom mohli na tuto třetinu sázet s nadějí, že na ruletě skutečně vyděláme, protože je pouze 5procentní pravděpodobnost, že ruletové kolo je vyváženo dobře a že to byla jen prostá náhoda.
Posunutí hranic na 99 %
Tabulka 2 má stejnou logiku jako předchozí tabulka, avšak zvětšuje oblast přípustných hodnot na 99 procent a kritickou oblast snižuje na pouhé 1 procento. Nyní to přeložíme. Podíváme-li se třeba opět na souřadnice [1 číslo a 10 000 spinů], pak 300 výskytů určitého čísla je ještě „v normě“ – kolo považujeme při této pravděpodobnosti za vyvážené, na rozdíl od předchozího příkladu, kde již šlo o kritickou hodnotu.
Dokonce ještě 309 spinů je OK. Jinými slovy: pravděpodobnost, že jedno číslo padne maximálně 309× (0× až 309×), je 99 %, a tedy pravděpodobnost, že jedno číslo padne 310× nebo více, je pouhé 1 %!
Pokud by nějaké číslo padlo 310× a více, pak na 99 % je kolo nevyvážené (není náhoda, že číslo padá tak často), resp. je jen 1procentní pravděpodobnost, že by kolo skutečně vyvážené bylo a časté padání tohoto čísla byla pouhopouhá náhoda. Na toto číslo by pak bylo vhodné opakovaně sázet a s největší pravděpodobností vydělávat.
Tabulka 2: Kritické horní hranice pro různé úseky kola a počty spinů (pravděpodobnost 99 %)
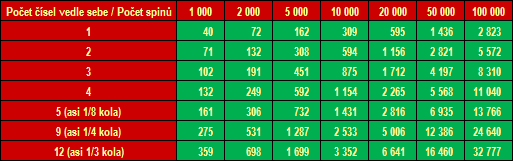
Stejný závěr platí i pro různé úseky ruletového kola. Například budeme-li pokrývat asi 1/4 kola (sázet na 9 sousedících čísel), při 20 000 spinech je 99procentní pravděpodobnost, že čísla z této 1/4 kola padnou dohromady maximálně 5006×. To opět znamená, že je jen 1procentní pravděpodobnost, že by tato 1/4 kola padla 5007× a více – v tomto případě by kolo bylo možné považovat za nevyvážené, protože je jen 1procentní pravděpodobnost, že by kulička padala do této 1/4 kola naprostou náhodou.
Závěr
Snad nejste zklamáni, že jste zde neobjevili senzační, zaručený a bezpracný návod, jak vydělat v ruletě. Žádné zázraky vám nebudeme slibovat nebo předstírat, že kasina jsou charitativní organizace. Přesto by vás mohlo zajímat, že existuje jedna teoreticky (!) neporazitelná strategie v ruletě.
Návod uvedený na této stránce je reálný, není bezpracný a umožňuje vyhrát i v praxi. Reálný, protože pracujeme se statistikou a pravděpodobností. Není bezpracný, protože vyžaduje získání a zpracování dat, což ale nemusí být problém, jsou-li data v elektronické podobě (řada posledně vytočených čísel) k dispozici, protože jejich roztřídění je záležitostí několika minut v Excelu. A vyhrát opravdu můžete, objevíte-li v nich určité anomálie (i když je to nepravděpodobné) – to snadno zjistíte podle našich tabulek.
Mohlo by vás také zajímat
- „Zaručený“ výdělek v ruletě;
- Teoreticky vyhrávající ruletová strategie;
- Jak obrat sázkovku při kurzovém sázení;
- Jak vyhrát v loterii Šťastných deset;
- Deziluze hráče rulety – jásat, když dlouho nešla jedna barva?
- Kolik zatočení rulety stačí k tomu, abyste s téměř jistotou začali prodělávat;
- Statisticky nejlepší sázka v ruletě;
- Ruletní systémy;
- Testy ruletních systémů a sázek.
